一、招生要求

1.参加过2021年普通高等学校招生全国统一考试，2021-2022年度本市普通本科高校本科在校在籍一年级优秀学生。

2.学生一年级所修课程考试成绩均须及格（含第一学期补考及格），且符合本市普通高校招收插班生的条件，经学籍所在普通高校同意后可以报考。

3.每位学生只能报考1所试点高校，学生学籍所在高校教务部门只能为每位学生出具1份相关证明。

二、招生专业

材料科学与工程

学科简介：

“材料科学与工程” 隶属于上海理工大学材料与化学学院。本专业以材料科学为基础，以新能源材料、环境功能材料、高分子复合材料、纳米材料加工、稀土功能材料等为方向，培养学生重点掌握材料科学与工程领域基础理论、专业知识和实验技能，掌握材料制备技术与结构表征、性能分析方法，培养具有“工程能力、创新能力、国际化视野”的材料行业工程技术和管理人才。

毕业就业：

上海理工大学材料科学与工程本科生就业去向大多是从事新材料行业相关企事业单位的生产设计、研究开发、项目管理等工作，在新材料、汽车、先进制造、半导体、冶金、化工、航空航天等行业或相关领域从事生产、设计、研究、开发、质控、咨询和管理等工作。

一大批优秀毕业生考入清华大学、复旦大学、上海交通大学、同济大学、浙江大学、中国科学技术大学、美国西北大学、美国康奈尔大学、曼切斯顿大学、悉尼大学、香港科技大学等国内外知名高校继续深造。

师资力量：

该专业拥有硕士学位授权点。所隶属的研究系所下正教授19人，已经形成了一支由国家百千万人才国家级人选、全国优秀教师、国务院特殊津贴专家、中科院百人计划、上海市领军人才、英国皇家化学会会士等高层次人才等优秀教师引领的师资队伍。

三、考试科目

四、考试题型

五、考试难度

英语难度分析：

上海理工大学插班生英语考试的水平是大学英语四级高分水平.本文具体到各项加以分析.

第一部分 词汇与结构

基本词汇量要达到5000,被动词汇量最好突破6000.本题考查的词汇是四级高频词（约500个）的具体用法和常见搭配.

第二部分 选词填空

采用十五选十题型。本部分主要考查考生结合上下文内容对文章中词汇的理解能力。

第三部分 阅读理解

阅读理解难度系数略高于英语四级，主要难度体现为在有限的时间内阅读四篇的文章。大约每篇文章用时10分钟左右，考生应该在把握全文脉络的前提下快速寻找线索和依据，对于细节题，要通过题目中的定位词找到文章的依据，并通过同义互替的方法确定正确选项。而对于主观题，比如主旨题，判断题，推理题，需要学生能够从全文当中寻找分散的线索，通过分析关键词，判断单词褒贬以及表达是否绝对片面等角度确定答案。

第四部分 完形填空

完形填空考察考生三个方面的能力： 第一考生应该具有通读文章快速了解文章大意的能力， 第二考生应该具有通过精读，揣摩上下文的含义和词性的能力。第三，考生应该具有分析段与段，句与句之间的逻辑关系的能力。考试可以选择考研英语二的完形填空进行相关训练。

第五部分 中译英

本题型模仿英语四级段落汉译英，主要考察学生能否利用四级词汇量根据中文进行英语翻译，在翻译技巧上是以直译为基础，意译为辅。同学们可以利用历年四级段落翻译真题进行训练。注意在翻译过程中首先要保证不要出现低级的拼写或语法错误，不要使用没有把握的英语表达。在汉语信息全覆盖的前提下，可以使用固定句型结构或采用复合句。

第六部分 英语写作

英语写作主要采用命题作文和漫画作文形式，考察学生在切题的情况下使用英语通顺表达自己意思的能力。文章采用夹叙夹议的形式，在英语表达基本正确无误的情况，考察语言文字是否通顺、连贯、论述是否合理有序。要注意卷面整洁，标点符号，文章分段等细节分，力争给评卷老师留下好印象

数学难度分析：

一.函数、极限、连续

00001. 准确掌握基本初等函数的性质及其图形；

00002. 会建立简单问题的函数关系，并确定其定义域；

00003. 理解极限的定义及其性质；

00004. 理解两个极限存在准则(夹逼准则和单调有界准则),并能利用它们证明简单的极限问题；

00005. 熟练运用等价无穷小替代、络必塔法则等方法求极限；

00006. 理解函数在一点处连续的三种等价定义方式；

00007. 会求函数的连续区间，判断函数间断点的类型；

00008. 理解并掌握闭区间上连续函数的主要性质。

二.一元函数微分学

00001. 清楚导数和微分的概念及函数可导、可微、连续之间的关系；

00002. 熟练掌握导数的四则运算法则和复合函数的求导法则，掌握隐函数和由参数方程确定函数 的二阶导数、特殊函数的高阶导数、幂指函数导数的计算方法；

00003. 理解 Rolle 定理、Lagrange 定理、Cauchy 定理、Taylor 定理(公式)的内容和意义，能利 用这些定理证明一些特殊点的存在性，或证明恒等式及不等式；

00004. 能利用导数解决函数的单调性和极值、曲线的凹凸性和拐点、方程根的存在性、函数的最 值等问题.

三．一元函数积分学

00001. 理解原函数与不定积分的概念；

00002. 会用第一换元(凑微分)法求不定积分，能灵活运用第二换元法求不定积分；

00003. 熟练掌握分部积分方法，能利用递推或循环运算等方法求不定积分；

00004. 会求简单有理函数和简单无理函数的不定积分；

00005. 理解定积分的定义；清楚定积分的性质(线性性质、保号性质、积分区间的可加性、积分 中值定理等)；

00006. 理解变上限积分的定义、性质及求导方法，清楚原函数存在定理的内容；

00007. 熟练运用 Newton-Leibniz 公式计算定积分；

00008. 会利用定积分的换元法、分部积分法计算积分，计算简单的反常(广义)积分，讨论简单反 常积分的敛散性；

00009. 会求平面图形的面积、平面曲线的弧长、绕坐标轴旋转的旋转体体积、变力作功、液体的 压力；

10. 能利用定积分的性质、积分中值定理、原函数存在定理证明有关问题. 四．常微分方程

00001. 会求解变量可分离的方程、齐次方程、一阶线性方程、Bernoulli 方程和全微分方程；

00002. 清楚高阶线性微方程解的结构；

00003. 掌握高阶常系数线性微分方程的解法；

00004. 能用微分方程求解简单的应用问题.

五.空间解析几何与向量代数

00001. 掌握向量的基本运算；

00002. 掌握平面方程和直线方程建立的方法；

00003. 会求点到平面之间的距离或点到直线的距离；

00004. 会运用平面束求解相关问题.

六.多元函数微分学

00001. 会求简单多元函数的极限；

00002. 理解偏导数与全微分的概念，清楚偏导数存在与可微、连续之间的关系；

00003. 掌握多元复合(含抽象)函数的求导法则，会求隐函数(包括由方程组所确定的函数)的二阶 偏导数；

00004. 能利用偏导数求解曲面的切平面与法线、空间曲线(包括方程组型)的切线与法平面、方向 导数、梯度、散度和多元函数极值等问题.

七.多元函数积分学

00001. 掌握二重积分的计算方法(直角坐标、极坐标)和三重积分的计算方法(直角坐标、柱面坐 标、球面坐标) ；

00002. 能利用二重积分计算立体的体积、曲面的面积；

00003. 掌握两类曲线积分的计算方法，清楚 Green 公式成立的条件；

00004. 会用 Green 公式计算一些曲线积分，掌握平面曲线积分与积分路径无关的判定方法，并 用这一结论计算(或简化)某些特殊的对坐标的曲线积分。

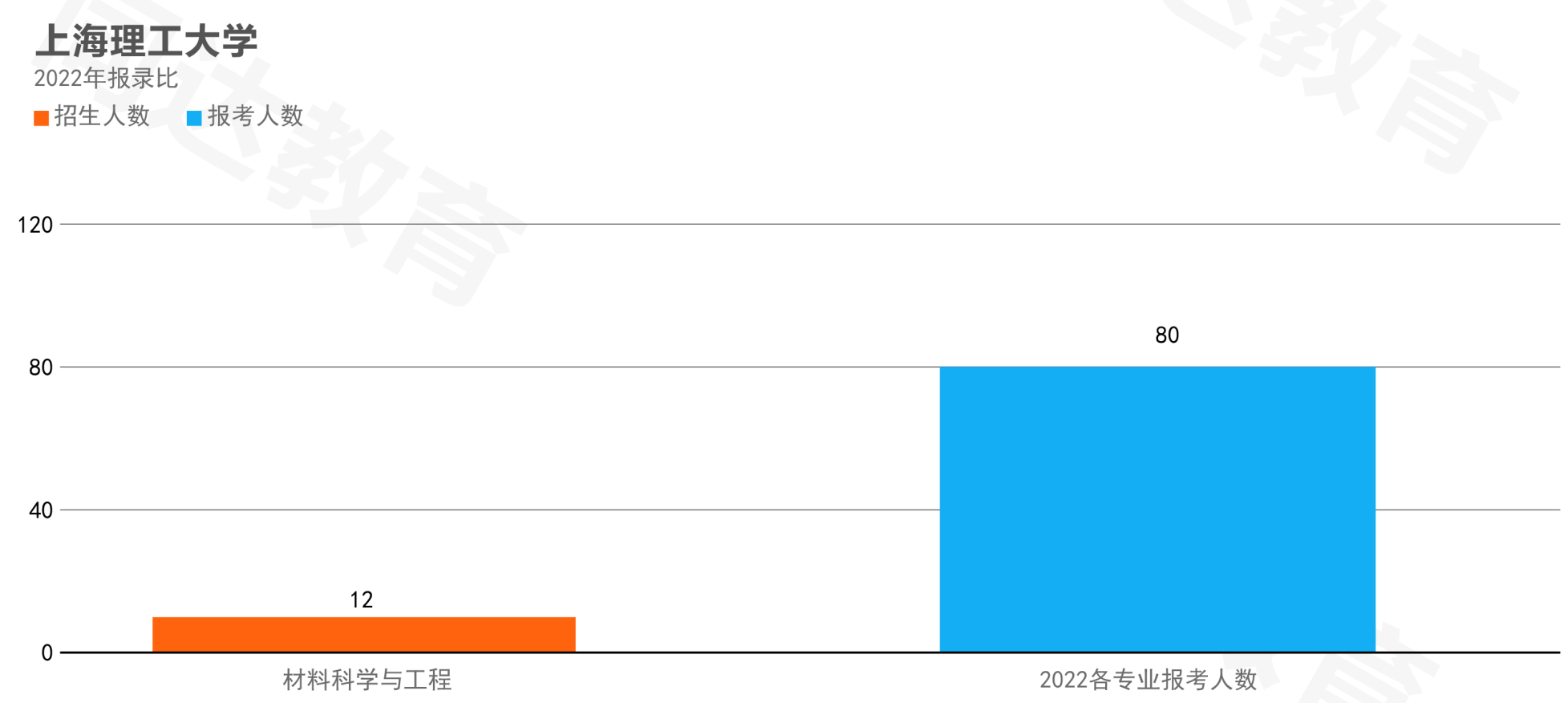
六、报录比

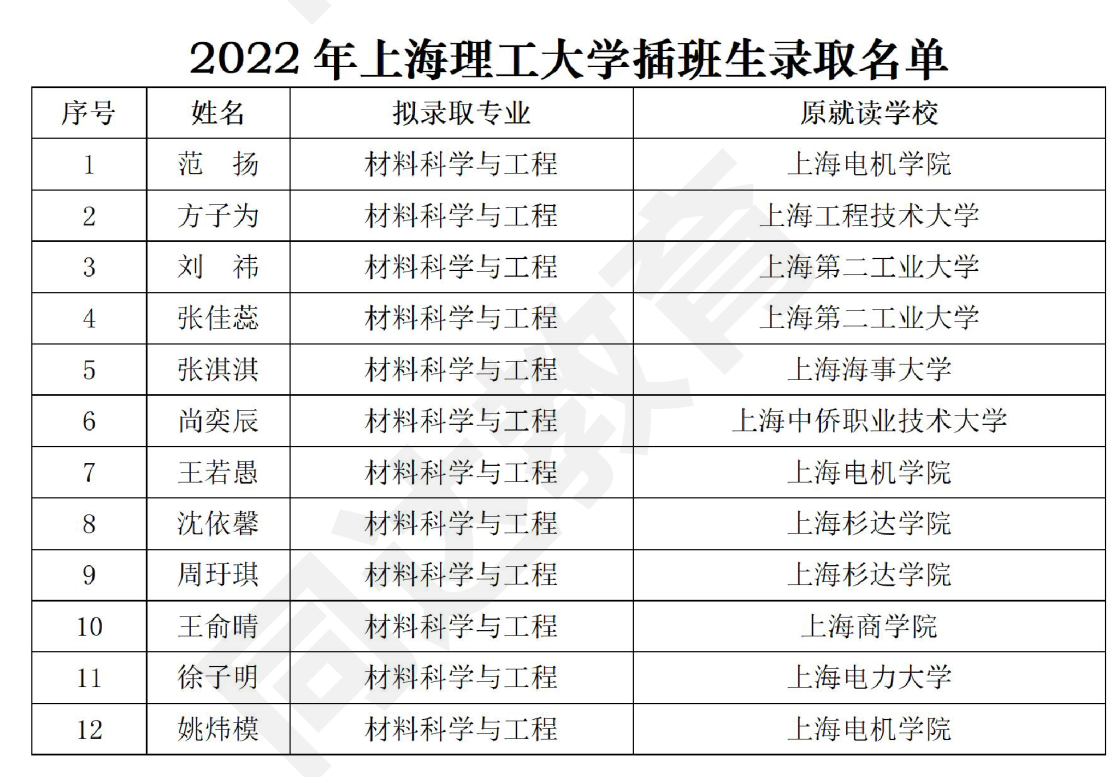
七、录取名单